Here we see how the alfo-theory of evolution is itself evolving…
in reverse chronological order
28-sep-18 VERSION 33.0 5d subdims inside 5d

13-jul-2018 ver 14.1 PXQ of NEZDEV
2013 mayan 7 spin 200
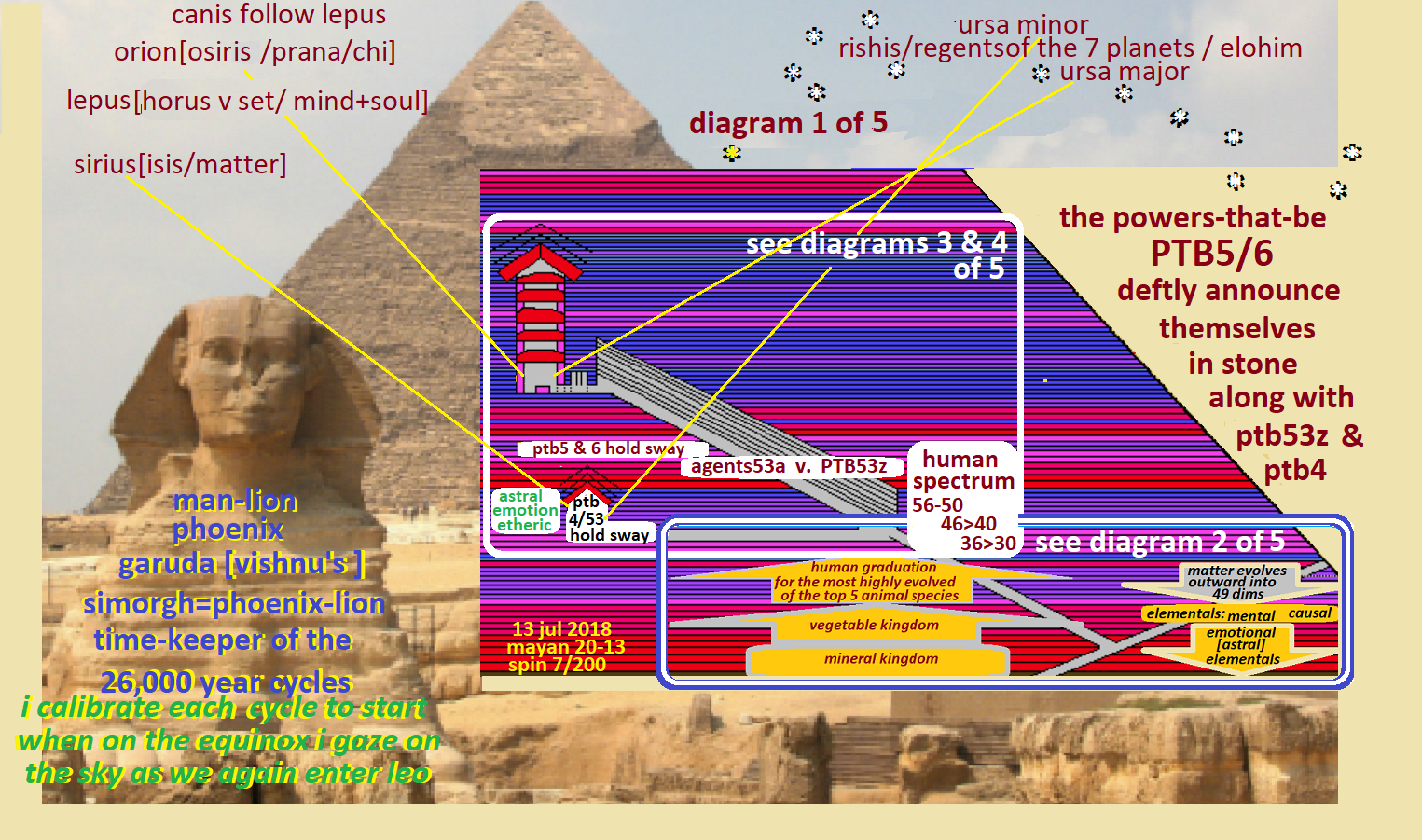
PXQ of NEZDEV ver 13
25 jun 2018 = 2013 mayan 7 spin 182
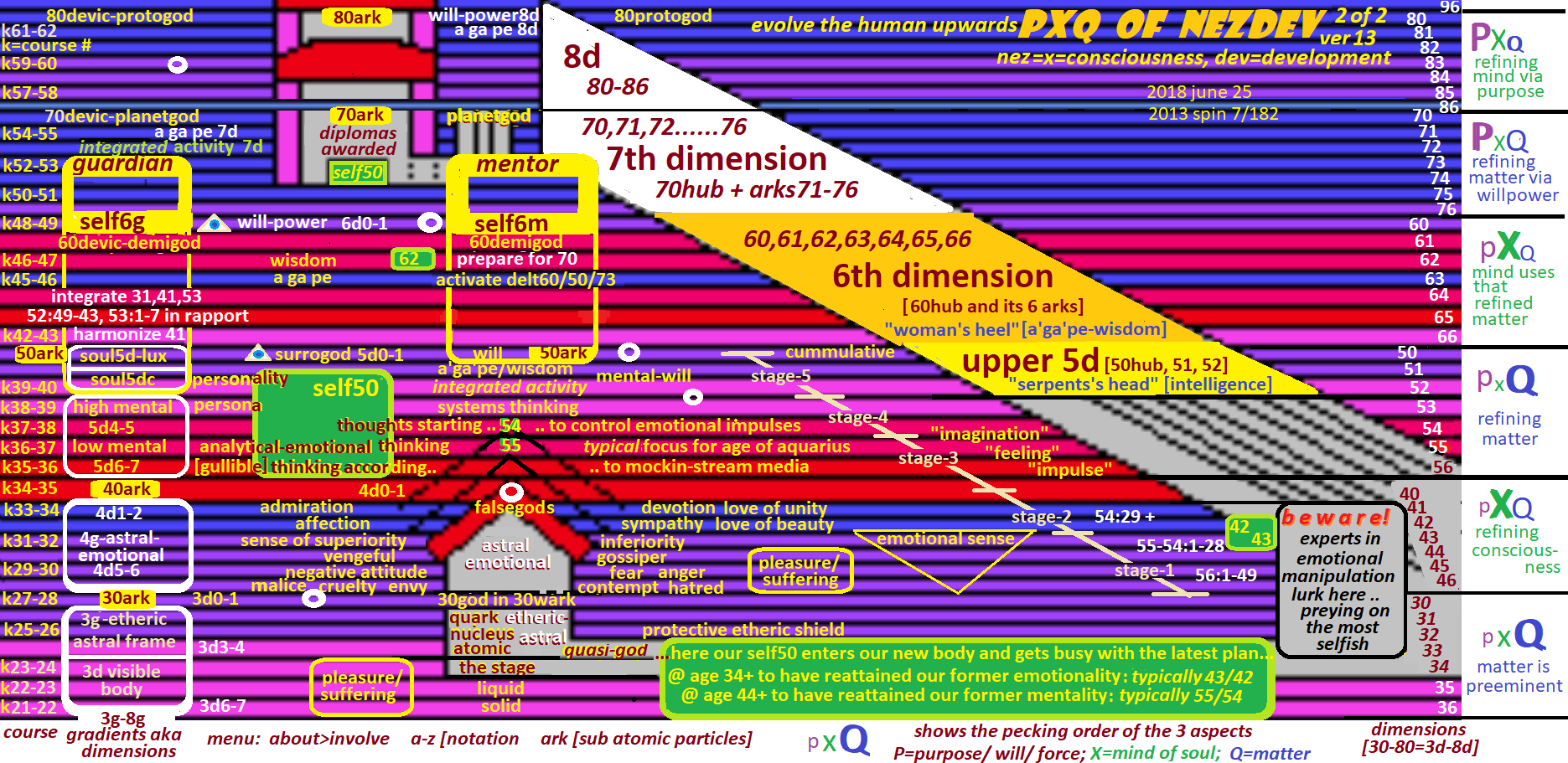
ALFO [ERSTWHILE] PHYSICS ver 12
11 jun 2018 = 2013 mayan 7 spin 168
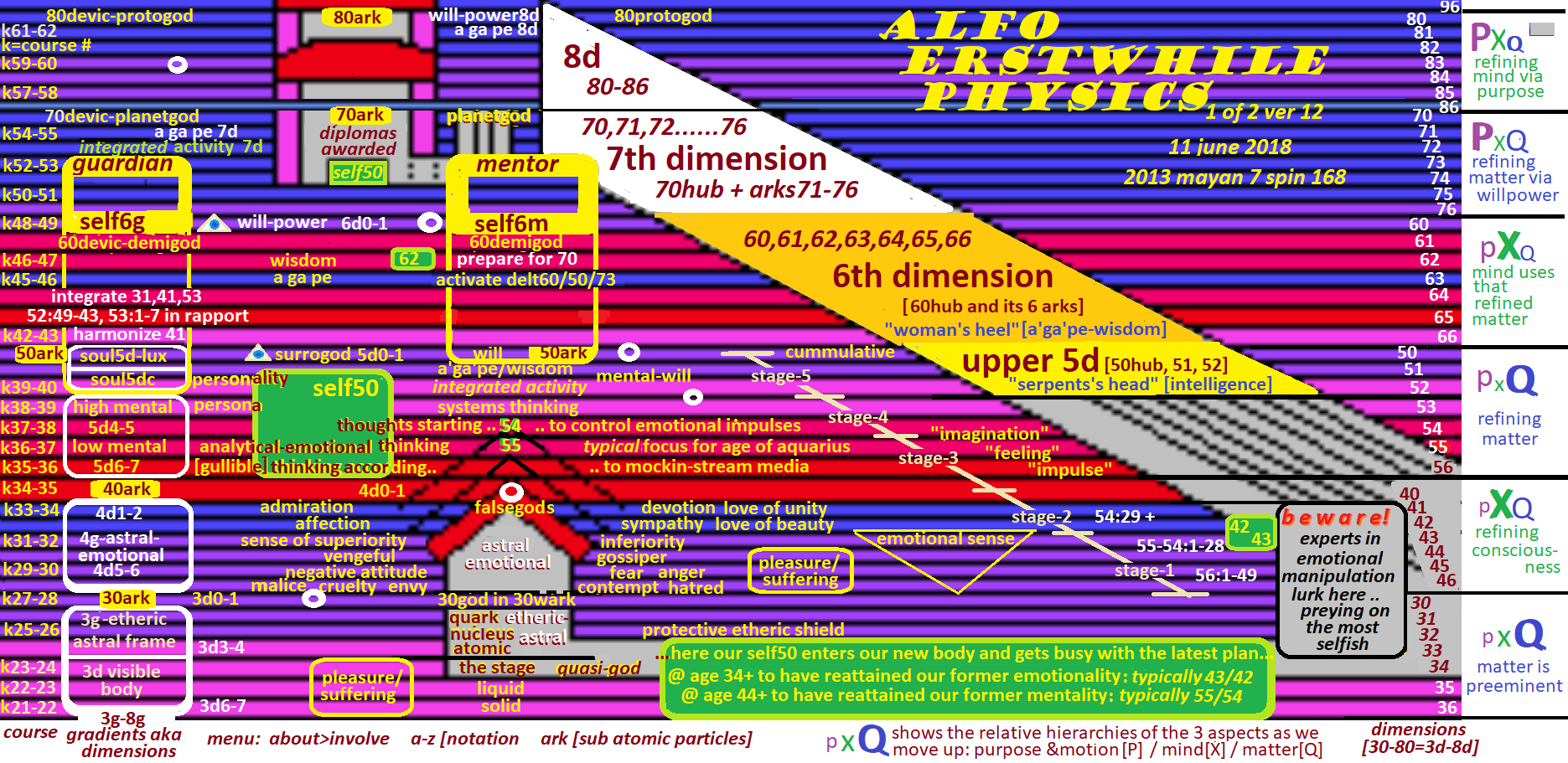
ALFO SUPERPHYSICS ver 11
26 may 2018 jun 2018 = 2013 mayan 7 spin 152

ALFO-THEORIES ver 4.0 / decode-8
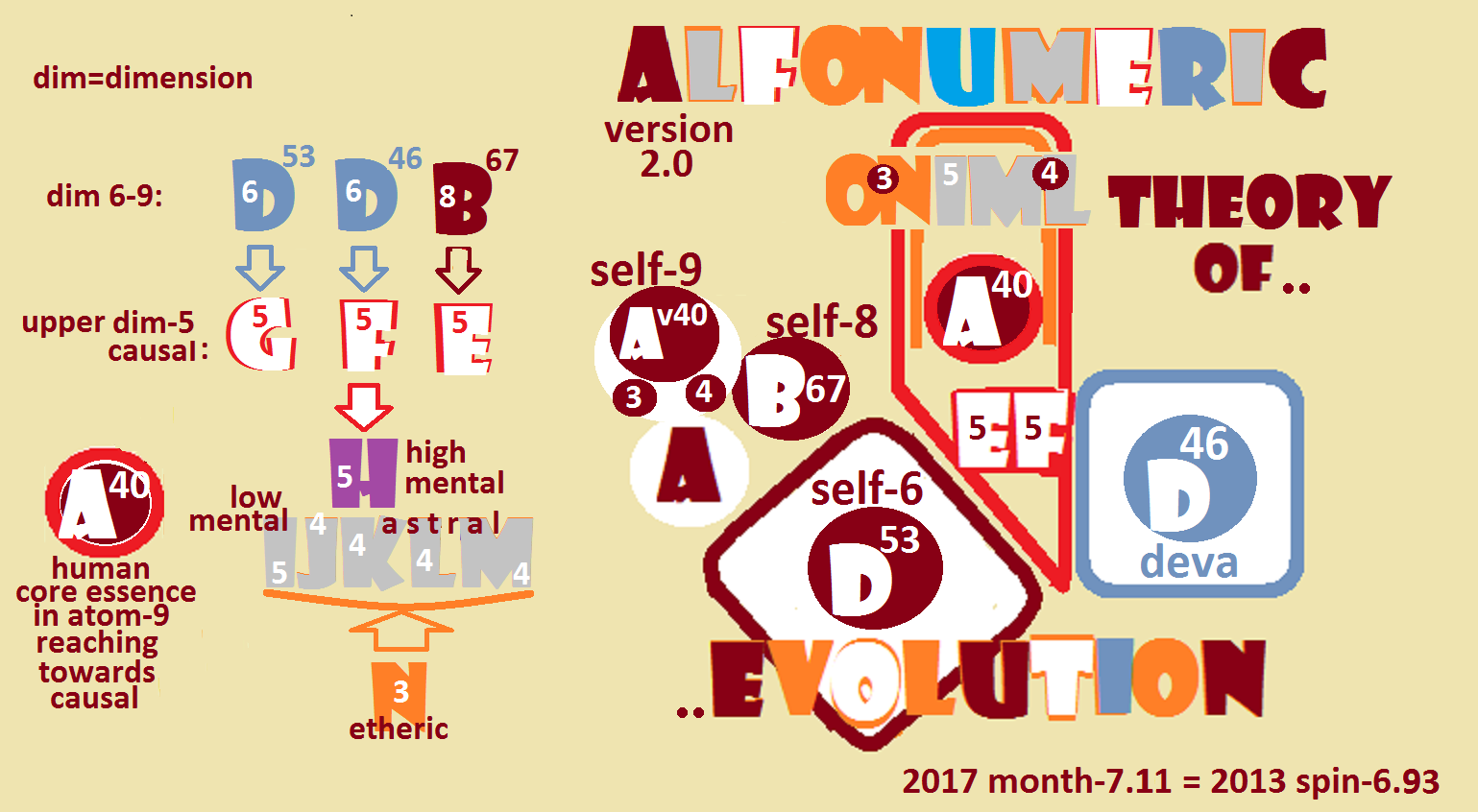
The term dimension takes on a whole new meaning. Instead of relating dimensions to the planes themselves, it makes much more sense to reserve the term for the sub-planes instead.
The clincher for this modification lies in the one-to-one correspondence between the number of subplane and the number of spirillae.
The current trending of evolution is firmly focused on the 4d-spirillae of the lower 6 subplanes., and small minority of us are busy activating on the 5th spirillae of the 5th subplanes.
The wark on each of the highest subplanes need all 7 spirillae activated since they are the supremo-warks overseeing all subplanes.
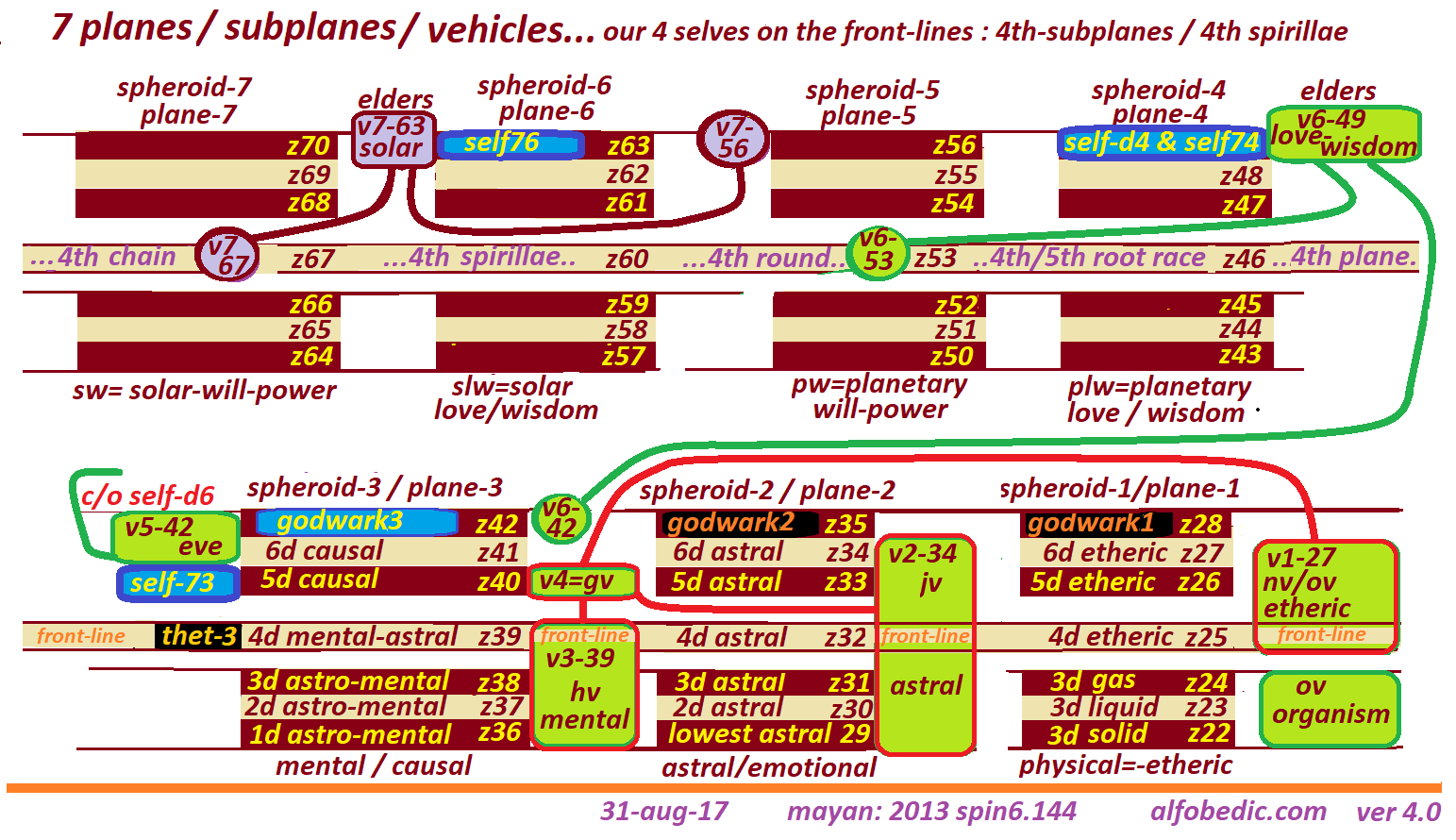
ALFONUMERIC ver 3.0 / decode-6
A new level of mathematical notation is introduced as inspired by the number of pomegranate seeds (4 and 6) mention in the greek and roman myths. So this website will have a more detailed exposure to the mathematical notation.
This picture is now out of date and numerical notation can be ignored see the new one here.
THE 4 CHALLENGES
Here we see our human essence fighting on 4 fronts with 4 challenges attempting to:
- discriminate between the angel presence using energies from realms b, d, e, f, g on levels z40-z67 and the dweller on the threshold somewhere between levels z25 – z39. The resultant maya is a combination / integration of the next 3 localized challenges.
- devitalize the problematic instincts on the etheric levels z25-z27
- dissipate the glamor and illusions on the astral levels z29-z34
- dispel the illusions and fictions on mental levels z36-z39
We are being activated from below on our etheric level N and from above via realms e, f, g = levels z40-z42
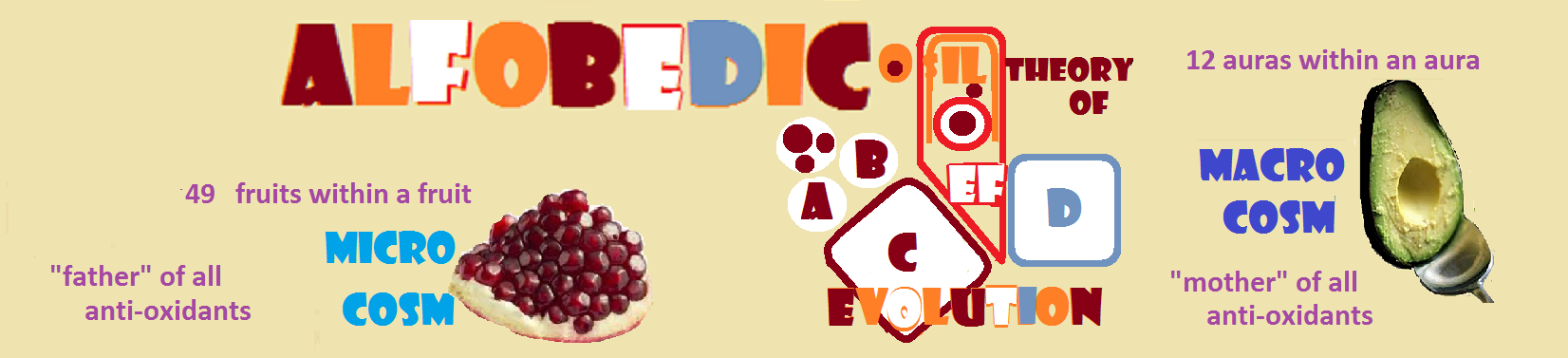
ALFOBEDIC ver 2.0 / decode-4
The solar angel gets her rightful place in the title.
ALFOBETIC ver 1.0 / decode-3
I was inspired by the 9 points of the 3 triads of diagram up.
One glitch was that letter d is missing and is instead replaced by “t” for triad.

end